I'm not going to answer this question for you---but do think about it. Eugene Calabi, one of Penn's most distinguished emeriti (who just celebrated his 90th birthday) and someone well worth listening to, is fond of saying "math is like science fiction." The reason he says so is that, in science fiction, just like in mathematics, the bounds of what is real is no obstruction. In math, you can take limits to infinity, or perform some operation ad infinitum, and likewise find no obstruction. I'd like to point out some other similarities between math and fictitious universes.
The Seirpinski Triangle
The Koch Curve
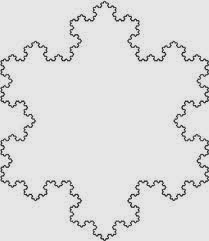
The Koch Snowflake
Lightsabers don't exist in the real world, but there is nothing stopping them from existing in fiction. In fiction Peter Parker is Spider Man (Spider Man exists!) and not just that but he winds up with Mary Jane; Elizabeth has her happy ending with Mr. Darcy (yes I had to look that one up---it's been a while since 10th grade English); Silas Marner finds his gold, though not the same gold he lost. All of this is a bit Walter Mitty---the point is that in fiction, or shall I say in good fiction, there is nothing stopping the imagination from traveling where ever it wills. The only constraints are the story's internal logic, and the natural constraints of character and common sense.
And inside of mathematics, what stops us from going where we want to go? What wild extremes can we explore, what great structures structures can we build? What finesse of detail can we obtain?
A piece of the Mandelbrot Set, a fractal of the early computer age.
In math the utmost extremes are open to us. And by utmost, I mean beyond the ridiculous, beyond anything our imaginations can readily conjure up---I mean nothing less than infinitude, or the infinitesimal, itself.
Fractal artists exists today; this is an example of such work.
A segment of a Julia set.
Take fractals as an example. In building our fractals, we took a simple set of instructions, and applied them again and again and again. In reality, you could only do this a certain number of times before the lines became too small for your pencil, or your computer ran up against its limits of floating point precision. But these are physical constraints, not logic constraints. in the realm of pure thought---of formal reasoning---there is nothing blocking you from carrying out a set of instructions infinitely often. The result of a simple process carried out to the absurd (that is, carried out to infinity) is in many cases the creation of patterns of unrivaled intricacy.
A Fractal Ball
Today fractals are used extensively in computer graphics; for instance landscapes, cloudscapes, etc are constructed with fractal techniques.
A Fractal Landscape
The first "fractal" artists was probably M.C. Escher himself, who mostly worked before the widespread availability of computers---he crafted his works by hand. Here is an example of a fractal-like piece of his:
Small and Smaller (1956)
Today the world of fractal art is immense, in part thanks to the video game industry. Works range from the abstract
A selection from http://www.fractal.art.pl
to the representational
A fractal tiger.
So yes, in a way mathematics is like fiction. But math is not even limited by what can be imagined---it has just one law: the law of the nuos, of formal reasoning itself.










No comments:
Post a Comment